本文轉自混沌巡洋艦
最近冠狀病毒的傳播成為家家戶戶關心的重點,同時謠言滿天飛。病毒到底最后會感染多少人,我有多少風險被傳染是眾說紛紜。而這正涉及了一個人類歷久常新的話題 - 預測未知。也是機器學習和復雜系統科學研究的重中之重。
不懂模型的朋友往往會被網上各種不同的預測搞得時而信息滿滿時而悲觀絕望。事實上了解模型的第一步就是記住一句話:所有模型都是錯的, 但是有些模型是有用的。任何模型都是一定的假設加推理的結果, 都有一定的置信區間, 不加批評的相信模型甚至還不如沒有模型。了解模型的基本邏輯才是最重要的。那么我們這里了解一下基本的模型如何幫我們預測肺炎傳播。
一, 統計模型
首先能夠幫我們預測感染人數的是統計學模型,統計模型是數據驅動的預測模型,它能夠幫我們解決的一個首要任務是在信息不全(小樣本)的情況下, 預測樣本總體的情況。比如我們知道某個飛機上武漢病人有n個人, 你可否知道整個武漢的感染人數?這看似是一個不可完成的任務,猶如通過梧桐一葉去判斷天下秋至。但是從統計學角度這是可能的。
但是我們有一個數據確實已知的, 就是某個時間段內海外檢測到的武漢肺病病人個數。然后我們可以從這個人數估算整個武漢新型冠狀病毒肺炎的得病個數。看上去天方夜譚, 這個海外出行的人僅僅占總武漢人口的滄海一粟, 那么這樣一個數據有什么特殊之處?為什么不用武漢某醫院檢測到的病人個數?
這里面的理由是從這個小樣本到總人口存在一條數量記錄清晰完整的鏈條, 直到得到武漢市的整個人口。為什么?首先每日出入機場的人數已知, 前往出境的人數已知, 那么計算一段時間內從機場出境的人數就是已知的。這使得計算這部分人中的染病概率變得比較簡單(某段時間患病人數/總人數),一旦推測到這個概率, 那么我們就得到了這個人口總數。
這個方法取決于非常重要的假設:武漢所有地區和人群的患病概率一樣。事實上我們很容易想到這個假設是錯誤的。能夠有能力出境的人口所具備的特點顯然不同于武漢的總人口。而且這個模型只能監測某個特定時間窗口的人數, 而非隨時間變化的人數。
如果我們引入更復雜的統計模型, 比如貝葉斯網絡,會取得比剛剛說的簡單模型好的多的預測效果, 但是依然無法對感染人數進行動態預測。
最初期的對感染人數的推斷來自這種由小樣本反推大樣本的統計模型, 用這個方法得到武漢21號左右的染病人數在4029, 但是大家千萬不要對十位數認真因為這個數字的方差估計得有大幾千。雖然方差巨大, 總體看在節前三天4,5000的感染人數是一個合理范圍。
Estimating the potential totalnumber of novel Coronavirus (2019-nCoV) cases in Wuhan City, China
二, 動力學模型
如果想預測未來的感染人數, 那么動力學模型是無法繞開的必由之路。動力學研究的就是事物運動變化的因果關系。在這個學科視角下,我們把世界理解成一張相互作用的大網,而事物運動變化的原因,都可以從這張大網上通過求解微分方程找出。
動力學最初的一鳴驚人,是空前絕后的牛頓三定律的提出,而牛頓第二定律又是三定律的核心,只要有高中數學基礎的人就知道,它是力與加速度的關系,看起來不起眼,但是它包含了整個動力學的核心思維,是什么?是受力分析嗎?
No。第二定律的本質,是預測,而預測無窮盡的未來,你不需要太多信息,只需要知道此刻和與之最近的下一刻的關系(微分的思維,下一刻是一個極限的概念,恰好脫離此刻的時刻),所謂s(t+1)=f(s(t))。s代表state,即狀態, f就是由此刻的狀態得到下一刻的狀態的迭代關系。有了f和初始時刻的s,未來即確定。
動力學里最重要的是了解系統的維度也就是變量的個數, 它決定了系統的復雜度。
我們把類似的思維用到疾病防控的思維里來, 如果你要做一個模型預測疾病的走勢, 就首先要把這個問題簡化成一個維度較低的系統, 這里我們可以把人口切分為三分,易感人群, 感染人群和康復人群, 病毒傳播過程里感染人群會傳播易感人群會, 而某段時間又會恢復。我們把這三個變量相互影響的關系用微分方程刻畫,就得到一個簡單的動力系統, 這三個變量可以稱為S, I 和R。I感染S, 同時I可以恢復成為R。雖然傳播是復雜的, 但是抓住最核心的因素, 無非三個不同的人口群體, 易感, 感染和恢復, 好比把人群分成了三節車廂, 這三節車廂就是SIR, 通過分析人口在這三個車廂的遷徙就可以預測未來的患病人數變化(如下圖)。


SIR模型示意圖 和微分方程
首先我們可以看到系統的穩定點(也就是微分方程的不動點)是I=0, S=0, 也就是病毒最終會過去(好消息!)。然后呢, 我們可以預測出一個指數增長然后又降落的趨勢, 傳播越快, 結束越快, 整個人口被病毒過濾一邊, 經歷從S到I到R的流程。我們目前可能正在處于這樣的指數上升期, 大家可以觀測最近幾天疑似的人數變化。
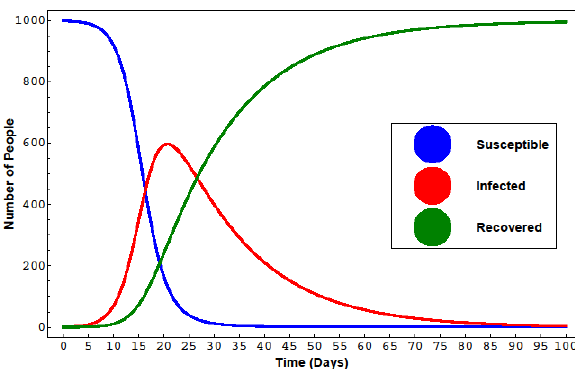
SIR模型中,處在不同狀態的人數隨時間變化的曲線
這樣一個簡單的模型告訴給我們以一種原始的信心,就是無論如何瘟疫總會過去, 而且病毒的感染率高,它起來的快過去的也快。這里的最核心參數就是傳播速度beta, 它決定了多少時間整個武漢人口將被過濾一遍疫情結束。beta取決于病毒的易感性和人群的接觸密度,它也是我們提出降低接觸密度控制傳播的最原始的基礎。
當然這里沒有考慮死亡率, 加上死亡率,那么最終得到一個被死亡過濾過的數量變小了的健康人口,就如同瘟疫后的幸存者組成新的聚落。
但是顯然忽略了眾多核心要素, 第一感染后的恢復者是否會在感染, 以及是否當接觸發生,同時I就變成了S, 也就是說接觸和感染發病幾乎是同時的。我們知道潛伏期是存在的, 那么加入潛伏期會對整個病患產生什么樣的影響?再者這里我們忽略了網絡效應,假定人口是封閉的。對于病毒, 這也不是一個特別合適的買賣, 因為經過一輪傳播自己也滅絕了。由此我們需要對整個疾病方程進行修正, 得到通常說的SEIR模型, 也就是在三個變量后加入一個E, exposed 也就是潛伏期的人。
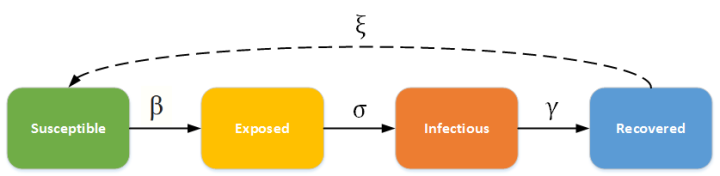

SEIR模型示意圖 和微分方程
新增的方程本質上加入了延遲, 它的作用使得動力學變得異常復雜, 甚至引入某種程度的波動性。它導致在疫情的某個階段我們完全看不到人數的增加, 而后面某個時間點突然開始增加。
病毒進化出潛伏期是非常聰明的選項,這僅僅是數學的世界, 在現實世界里,這個潛伏者的網絡會導致一部分人作為病毒傳播的緩沖(而且通常潛伏期是一個區間而不是一個固定時間,它可以使得疾病此起彼伏的發生), 在不被發覺的情況下移動到非常遙遠的地方,從而大大加速傳播的時間和空間距離。

seir模型可能的不同人口變化曲線
seir模型可能的不同人口變化曲線從病毒的角度看, 增加潛伏期也是非常明智的,因為增加的潛伏期意味著動力學可以進入一種長期震蕩狀態,通過潛伏可以在時間軸上傳遞更久的時間,有利用病毒自身的進化。利用類似SEIR的模型, 一些專家得到了武漢新型冠狀病毒的蔓延預測,以及平均每個人都周圍人傳播的R值。
Estimation of the transmission risk of 2019-nCov and its implication for public health interventions Biao Tang , Xia Wang , Qian Li , Nicola Luigi Bragazzi , Sanyi Tang , Yanni Xiao Jianhong Wu
在這篇文章里我們加入了更精細的對易感人群和隔離人群的刻畫, 從而也更貼近真實情況。最關鍵的利用蒙特卡洛模擬它給出了一個人平均傳播病毒的個數R=6.47一個十分可怕的數字。如果相信這個數字是真實的, 那么一個人傳播六個人, 不加防控的結果將十分可怕。
如果你感興趣還可以參考一篇更為悲觀的文章同樣用到了SEIR, 雖然文章中對R值的估計更保守:
Novel coronavirus 2019-nCoV: early estimation of epidemiological parameters and epidemic predictions Jonathan M. Read , Jessica R.E. Bridgen , Derek A.T. Cummings , Antonia Ho, Chris P. Jewell
盡管如此,動力學預測對我們理解問題的意義是重大的, 我們可以通過公式了解到影響傳播速度的是哪些要素, 比如疾病自身的傳染性和社會網絡的連接性, 這也可以指導我們做出正確的決策, 別如什么時候封城或者開城。但是, 如果要做到更精確的預測,比如疾病在某個地區的變化曲線,就不那么有效。
三, 交通網絡的影響
這時候我們必須借助網絡的力量。網絡即高維的動力學系統。網絡有很多層的含義, 在一個小區或社區里人們相互連接形成網絡,在城市和城市之間有立體的交通網絡。這些網絡是構成病毒傳播的第一層體系。整個網絡, 組成一個層級化的復雜系統。這時候整個傳播過程變得異常復雜, 每個個體只能傳播到相鄰節點,而人員需要靠交通網絡流動。這時候網絡結構本身的性質對傳播開始起到至關重要的作用。如果直接考慮個體, 整個模型將參數大到無法想象, 所以在考慮網絡的時候,我們不妨把每個城市節點的方程看成上面的SEIR模型, 然后考慮不同的城市間的耦合, 這樣我們仿佛得到了一個全部城市組成的動力學方程組。
這時候我們會發現城市交通網絡在傳播中的重要作用。首先我們會想到武漢是一個九省通衢的中心城市, 那么從這樣的樞紐型節點爆發,就比從其它節點有深遠的多的傳播力。當這整個社會網絡進化成無標度的小世界網絡, 病毒可以無閾值傳播。這突出的說明了網絡結構對病毒傳播的至關重要性。
Pastor-Satorras, R. and Vespignani, A. (2001) Epidemic Spreading in Scale-Free Networks. Physical Review Letters, 86, 3200.

無標度網絡上的疾病傳播
何為無標度網絡, 在古代社會, 社會網絡以局部的連接為主, 當一個社會分工變得越來越復雜, 就需要更多的樞紐承擔起物流中轉站的重擔, 比如武漢這樣的超大城市。這些樞紐會使得網絡的連接不再是局部的,而是呈現出一種重要hub(樞紐)和局部連接并存的形式, 樞紐和大部分樞紐都有連接,這樣的網絡稱為小世界網絡,類似的網絡結構在大腦和互聯網上也是類似的。小世界網絡的傳播特性決定了一方面它是一種十分高效的組織形式, 一方面比起局部連接的網絡它也更加脆弱,比如在病毒的傳播上。我們可以想象除了病毒之外還有什么可以打擊這樣的網絡系統,或許就可以從此次病毒防控中得到啟示。
Simulating SIR processes on networks using weighted shortest paths Dijana Toli?, Kaj-Kolja Kleineberg & Nino Antulov-Fantulin
同時這個理論給截斷中心城市提供了絕好的理論依據, 因為截斷中心城市,就可以將網絡從無標度網絡退化成局部連接的網絡,對病毒傳播起到非常大的抑制作用。這比防控鄉村或局部城市要來的高效的多。
四, 考慮信息傳播的網絡影響
事實上人們在談論病毒的過程中也改變了病毒傳播的動力學本身。比如一個消息傳遞到一個地方, 這個地方的傳播網絡自然就減弱了。如果考慮到信息和病毒傳播的耦合, 整個動力學系統就增添了新的性質。
在網絡時代, 信息的傳播是完全自下而上的自組織行為,信息流里的恐慌情緒會具有和病毒類似的傳播能力, 這種網絡情緒會如何和病毒傳播相互作用應該是一個新的學術問題。從目前看這種非理性的情緒某種程序也起到了阻斷病毒的作用, 因為過度行動肯定優于不行動, 雖然某些時候恐慌情緒引起的醫院擠兌也確實加重了傳播。
在很多時候, 信息傳播可能會比阻斷物理傳播有更低的成本,也是這個時代賦予我們的超級武器。
五, 考慮病毒自身的進化效應
之前的模型依然考慮的是病毒自身的基因是靜態的不變的, 事實上, 病毒通過每個人和整個社會網絡進行傳播,被殺滅的同時也迅速進化著(這點對于ncov 這樣的RNA病毒體現尤為明顯), 因此這是一場人和病毒的賽跑或者博弈。
在這個層次上,如果模型里只考慮靜態不變的病毒, 就沒有任何說服力。事實上我們的防控手段也在影響病毒的進化。病毒的基因本身的變化也應該被看做動力學系統的一部分。
這個問題就涉及超級傳播者, 超級傳播者的含義是一些年老體弱的個體好比病毒的超級培養皿, 加上長時間的醫學治療, 可能會使得病毒在這些個體上傳播超級多代,從而在它們身上得到更加強大的病毒。由于現代醫學的發達, 在整個人和病毒斗爭的治療周期里我們也給了病毒更多的進化機會, 某種程度我們在治療疾病的同時也在創造新的病毒。
何謂強大的病毒, 它體現在能夠和人打太極而不是簡單的致死率, 也就是潛伏期更長, 傳播更隱蔽, 不太高的致死率, 從而取得和人類共存,繼續協同進化(博弈)的機會。 在這個層級上, 我們不得不將博弈論納入我們的模型,而使得最后的模型成為一個復雜網絡演化加博弈模型。
六, 理解傳播動力學的實際意義
如果理解動力學僅僅解釋了我們已知的現象, 那么并不足以讓人們覺得這種建模是有用的。事實上, 建模的意義在于更加精確的預測和防控。這個時候深度學習的武器就不能被我們忘記。 我們有了動力學模型,加上一定量的數據, 就可以建立一個可以學習的模型, 從而根據數據不停的優化預測的精度, 這個預測不只是感染的總人數,還有每個地區的人數, 以及在什么時候需要采取怎樣的措施(強化學習問題)。
在病毒傳播的建模過程里, 我們看到一個貫穿不同層次的核心概念-網絡。病毒本身是一個RNA的分子網絡, 然后病毒入侵人體網絡使人得病, 而人作為社會網絡里的個體又傳播疾病。不同層級的網絡耦合在一起,每一層的網絡都是動態的,使得這個問題充滿了不確定性。這也是為什么當下的所有預測數據置信區間都很大, 同時有一些問題是我們永遠無法估計的, 比如病毒的變異究竟會趨于什么形態,是否某種更高致死率和傳染性的變種會在一個個人體進化爐里被孵化出來。
而最重要的一點,在于理解網絡動力學對疾病控制的啟發。如果我們知道了傳播的動力學, 我們就可以比較有效的控制一個復雜網絡,也就是阻斷疾病的傳播。比如如何根據病毒的特性制定最有效的阻斷策略, 同時不至于殺敵一千自損二千。從長遠看, 它要求我們把對大型疫情的控制, 看成社會網絡設計的一部分, 比如對高危傳播路徑(人畜)的控制, 對疫情信息的早期播放和傳遞, 在出現疫情后如何第一時間記錄和鎖定傳播路徑切斷, 以及如何用最有效的方法構建醫療網絡等等,這樣的長效措施將會把未來發生比冠狀病毒更可怕的傳播時候的社會風險降到最低。
原文鏈接:https://mp.weixin.qq.com/s/jHbHFXOQ89NQrSoSGYfYMw