卷積神經網絡的壓縮和加速
新聞鏈接:https://mp.weixin.qq.com/s/PfnEJpodnRACTcuoSiV8nQ
背景介紹
為什么要對網絡進行壓縮和加速呢?最實際的原因在于當前存儲條件和硬件的計算速度無法滿足復雜網絡的需求,當然也許十幾年或更遠的將來,這些都將不是問題,那么神經網絡的壓縮和加速是否仍有研究的必要呢?答案是肯定的,我認為對網絡壓縮和加速的最根本原因在于對高效率模型的追求,當前很多復雜網絡中的很多參數是冗余的,對實際模型結果沒什么貢獻,我們怎么能容忍這些無意義的參數竟然和有意義的參數享受相同的“待遇”——相同的存儲空間和計算時間。尤其當存儲空間和計算時間受限的情況下,我們更加無法容忍那些無意義的參數。當我們可以構造訓練出一種模型,其所有的參數都是不可替代的,那么壓縮和加速的工作就終于可以走向歷史舞臺了,但這種情況是不可能發生的,至少在近幾十年不可能發生,因為當前神經網絡對于研究者來說仍是一個黑箱。
神經網絡剛剛被提出來時,對于如何將其應用與圖像仍是個很大的問題,最單純的想法是將圖片按像素點排列成向量,再走多層感知機的老路,但由于參數太多,存儲不便,計算速度太慢,始終無法得到進一步發展。終于一個神奇而又簡單的想法逆轉了這個困境——偉大的權值共享,于是卷積神經網絡將整個模型的參數減少了若干倍。雖然由于當時硬件條件限制,對卷積神經網絡的研究也一度陷入瓶頸,直到2012年AlexNet一鳴驚人。但權值共享應該稱得上是神經網絡壓縮和加速的第一次偉大嘗試。卷積神經網絡也是權值共享的神經網絡的一種。接下來的模型加速和壓縮,都是針對卷積神經網絡模型的。
針對卷積神經網絡模型的壓縮,最早提出的方法應該是網絡裁枝,LeCun在1989年就提出根據損失函數對各個參數的二階導,來估計各個參數的重要性,再刪去不重要的參數。后來又是到2012年之后,壓縮方法更加多樣,總體大約分為4種:網絡裁枝、模型量化、低秩估計、模型蒸餾。下面SIGAI將對4種方法進行逐一介紹。
網絡剪枝
我們先來看看當前深度學習平臺中,卷積層的實現方式,其實當前所有的深度學習平臺中,都是以矩陣乘法的方式實現卷積的(如圖1左側):
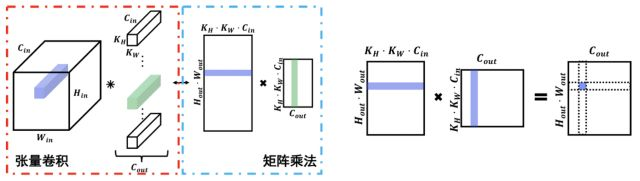
圖1 卷積與矩陣乘法
網絡裁枝有兩個大問題需要考慮:
第一,對輸出某一點進行裁枝,一定會影響到輸出的其他點。(如圖1右側),從輸出特征圖角度看,輸出矩陣(經過維度reshape可得到輸出特征圖)中的點Pij,實際是與輸入矩陣中的第i行連接的,同時連接權重為參數矩陣的第j列;從輸入矩陣(輸入特征圖經過im2col變換得到的矩陣)角度看,輸入矩陣的第i行與輸出矩陣第i行所有點都是連接的;從參數矩陣(參數張量經過reshape得到的矩陣)角度看,參數矩陣第j列為輸出矩陣第j列所有點的連接權重。假設我們對圖中輸出矩陣紫色節點裁掉1個連接,即令參數矩陣(中間的矩陣)紫色列中某個參數為0,那么根據之前的分析,該參數的刪去,一定會影響輸出矩陣虛線列中的所有節點。這就是卷積神經網絡裁枝的復雜性。
第二,若無規律的刪掉一些連接,即令一些參數為0,實際上無法壓縮,因為在網絡存儲中,0也是按32位浮點數存儲的,與其他參數的存儲量相同。所以我們不能僅僅將刪掉的參數設為0,而是要徹徹底底地刪掉這些矩陣。
最簡單的一種想法:直接刪掉參數矩陣的某一列,對應的就是刪掉一個filter,相應的輸出特征圖將少一個通道。而在下一個卷積操作時,這個輸出特征圖將變成輸入特征圖,帶入到圖1右側的輸入矩陣,少一個通道即少一個列,那么為了保證矩陣乘法正確,參數矩陣必須要對應刪去一行,即所有filter都要刪去一個通道,整體變化如圖2所示。從上述介紹我們發現:若對某層卷積以filter單位裁枝,那么到下一層一定會有以channel單位的裁枝,這就是filter-level裁枝(圖4中所示)

圖2 filter-level剪枝[1]
第二個想法:我們若將3*3的kernel刪成2*3或更小的kernel,對應到參數矩陣,即刪掉了若干行,同樣絕對有壓縮的效果,而這種裁枝并沒有改變channel的個數,雖然輸入矩陣的列數需要減少,但這是在im2col操作中進行的(以kernel和stride不同設置,會生成不同的輸入矩陣),對輸入特征圖與輸出矩陣沒有任何影響。
對第二個想法,我們可以進一步改進:如果將3*3的kernel刪成某個固定的形狀,例如下圖中,那么我們可以修改im2col操作,保證卷積的正確性,這就是Group-level的裁枝(圖4中所示)

圖3 另類kernel(白色為0值)
第三個想法:如果我們不急著刪去參數,而是將那些沒用的參數設為0,當整個參數矩陣中有很多的0時,稀疏矩陣閃亮登場,于是矩陣的乘法可以用稀疏矩陣的乘法來代替,從而起到模型壓縮和加速的效果。圖4中,Fine-grained,vector-level,kernel-level中一些裁剪方法,需要使用到稀疏卷積的方法來實現。
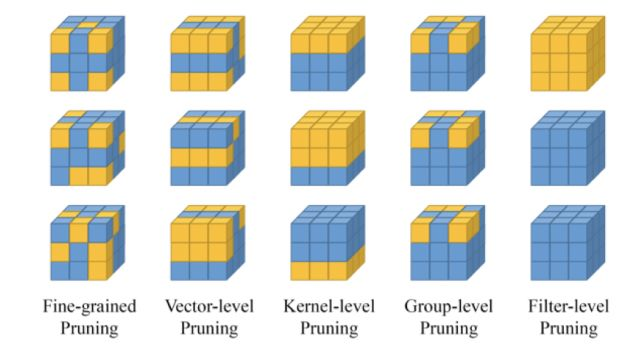
圖4 裁枝類型圖示[2]
上述是從矩陣方面,對裁枝方法進行了講解,其實我們忽略了一個重要的問題:究竟什么樣的參數需要裁掉呢?一般有兩種方法:損失函數對參數的二階導,和參數的絕對值大小。第一種方法,損失函數對參數的二階導越小,說明這個參數的更新對損失函數的下降的貢獻越小,說明這個參數不重要,可以刪去。第二種方法,參數絕對值越小,說明輸出特征圖與該參數幾乎無關,因此可以刪去。相比較而言,第一種方法是盡可能保證損失函數不變,對結果影響相對較小,但計算復雜;第二種方法是盡可能保證每層輸出特征圖不變,而不管損失函數,計算方便,但對結果可能相對較大。但無論哪種方法都需要對裁剪后網絡做參數調優。
低秩估計
低秩估計的方法其實就是運用了矩陣分解和矩陣乘法的結合律。此時我們仍需要回到圖1左側的示意圖:對輸入矩陣我們無法做分解,因為不同的前向傳遞中矩陣是變化的,但是參數矩陣是固定的呀,那么何不分解參數矩陣呢?低秩估計就是這么個想法:
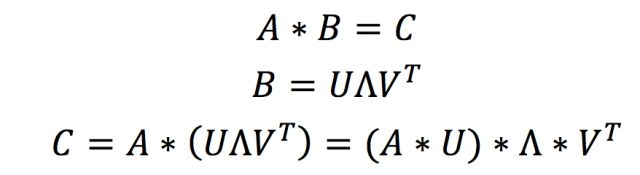
看上面的這個式子是不是感覺特別簡單,只要我們可以用若干小矩陣對參數矩陣進行估計,那么輸出矩陣就可以通過上面的式子得到。
在當前的很多對低秩估計的研究中,筆者認為奇怪的一點是:對矩陣分解后,將分解后的矩陣乘法又轉回成卷積操作,例如上式中將原參數矩陣分解成3個小矩陣,那么在實現中就是用3個卷積來實現分解后的矩陣乘法。筆者認為這種操作實際上是增加了計算量,因為卷積需要經過im2col過程才可以轉變成矩陣乘法,所以為什么不直接實現新的層或Op來做3個矩陣乘法呢?那么相對于用卷積實現,其實是少了2個im2col的過程。當然這是筆者的思考,還沒有經過實驗驗證,如果有不同的想法或者實驗結果,希望可以拿出來一起分享。
除矩陣分解以外,我們也可以直接對張量進行分解,而且卷積也符合結合律,那么上式中的乘法即變成了卷積,矩陣變成了張量,如下式以tucker分解為例:
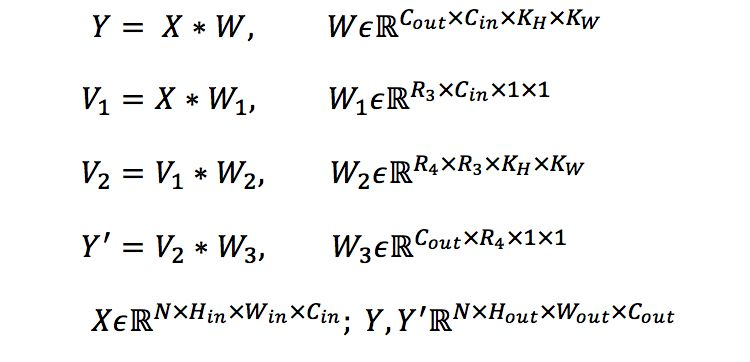
同樣可以得到更小的參數張量和與原輸出相似的輸出矩陣。下面我們以Tucker張量分解為例,分析一下低秩估計方法的壓縮和加速效果。Tucker分解是對張量直接進行分解,其分解效果如圖5所示
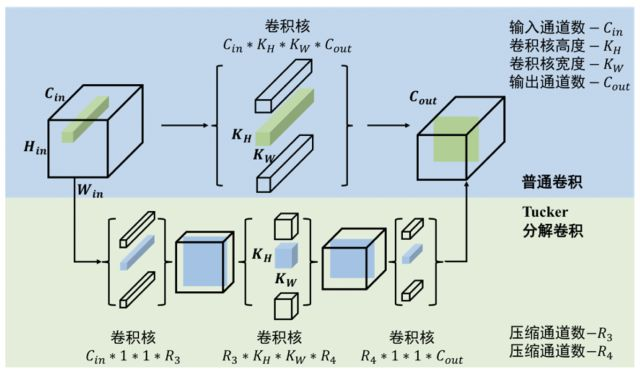
圖5 Tucker分解
原卷積經過分解成3個計算量更小的卷積,卷積核通道數如圖中所示,那么分解前后計算量為
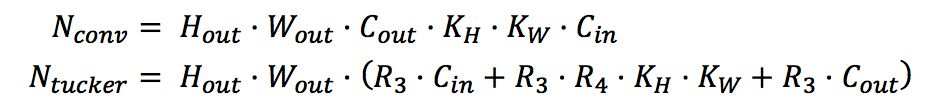
式中`N_(conv)`表示普通卷積的計算量;`N_(tucker)`表示分解后3個卷積的計算量之和。為了計算方便,且一般情況下`R_3`,`R_4`相差不大,不妨設`R_3=R_4=_R`;一般情況下Cout與Cin之間成倍數關系,通常為2倍,不妨設為n倍關系;且理論加速效果與計算量大小成正相關,不妨設通過tucker分解理論加速m倍,即分解前計算量至少是分解后計算量的m倍;求R與C之間關系,不妨設為k倍,于是有
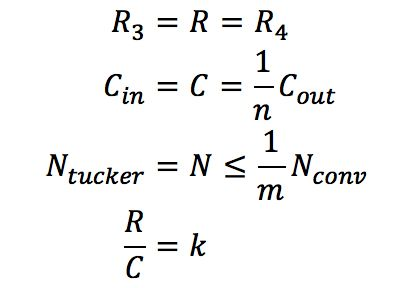
可求得

由上式可知,`K_max`關于n遞增,關于`K_HK_W`遞增,關于m遞減。即在保證加速程度不變,即不變的條件下,該卷積操作的輸出特征圖通道數相比輸入特征圖通道數越多,即`K_HK_W`越大;卷積核空間維度越大,即越大,tucker分解的中間層的特征圖通道數可以越接近輸入通道數,即可以更大。在通常的網絡結構中,值一般取1或2;`K_HK_W`一般取1*1或3*3,針對一般取值,下面的表格中給出了`K_max`的解。
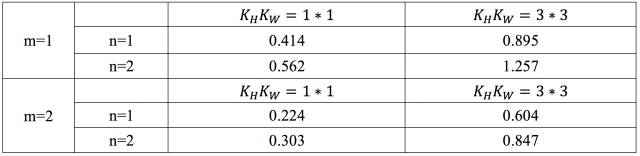
由表所示,若要求加速至少2倍,在卷積核大小為3*3,卷積輸出通道數等于輸入通道數時,tucker分解的中間卷積通道數最大是原來的0.604倍。當然中間通道數越小,可實現的加速和壓縮效果越好;而為了保證準確率,中間通道數越大,分解后的張量還原回原張量的誤差越小,這就是速度與準確率之間的權衡,也是低秩估計方法的共性。
低秩估計的方法的優勢在于,沒有改變基礎運算的結構,不需要額外定義新的操作。分解后的網絡仍是用卷積操作來實現的,所以其適用面比較廣泛。分解方法多種多樣,任何矩陣或張量分解的方法都可以應用其中,但一般分解后的網絡都需要參數調優,以保證分解后網絡模型的準確率。
低秩估計方法存在一個待解決的問題,就是保留多少秩是不明確的。保留太多的秩可以保證準確率,但加速壓縮效果不好;保留秩太少,加速壓縮效果好,但準確率很難保證。曾經有工作提出先訓練低秩的參數矩陣,即在損失函數中加入對參數矩陣秩的考慮,然后再對訓練好的低秩網絡做低秩估計,由于本身參數矩陣中很多列向量都是線性相關的,所以可以保留很少的秩進行分解。
模型量化
無論是網絡裁枝,還是低秩估計,我們從矩陣乘法入手(圖1很重要),想方設法將參與計算的矩陣變小,直觀地減少參數量和計算量。相比于前兩種方法(他們注重計算數量的減少),模型量化則著眼于參數本身,實際上模型量化的大多方法并沒有改變模型的計算數量。
如果我們可以用有限的幾個參數來估計連續的實數域,那么就不用每個位置都存參數了,我們只需要存儲有限的幾個參數,和每個位置對那幾個參數的索引不就行了么?索引可以用整數來表示,如果我們存儲的參數為256個,那么只需要8-bit整數就可以索引,相比于所有位置都存32bit的浮點數,模型的存儲量可以下降到原來的1/4。
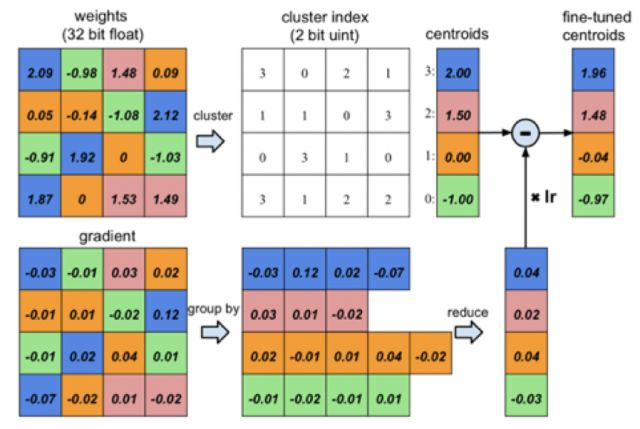
圖6 參數聚類編碼[3]
再進一步,如果我們將計算也改成8-bit整數的計算,移動端和嵌入式設別的CPU處理整數的計算速度要快于浮點數,那么這種網絡不就可以在不改變連接數和參數個數的前提下,壓縮和加速網絡了么?這種想法就是模型的定點化。
將32-bit浮點數運算轉化為更低位的整數運算,常見的是8-bit整數運算或1-bit二值運算。思想十分簡單,以8-bit整數為例,記錄當前參數的最大值和最小值,設為mini, maxi。則所有參數量化結果為
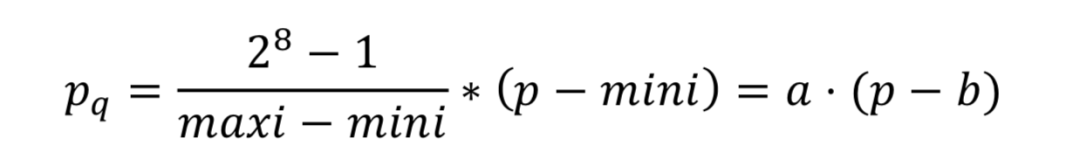
于是所有浮點數都可以轉化為整數運算,但這種方法存在2個困難:第一,若兩個值的mini,
maxi值不相等,運算比較復雜;第二,由于存在系數和偏差,所以浮點數的加法與乘法需要額外一些運算才能還原。對這兩個個問題,我們可以采用簡單的代數運算的得到結果,以乘法為例。
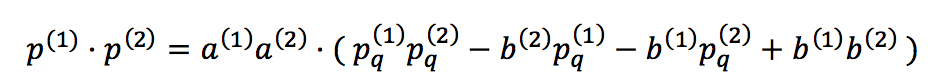
有興趣的讀者可以進一步參考gemmlowp庫中的說明文檔,或者自己推導一下加法的運算。那么基礎理論就到此為止,在當前的深度學習平臺中,Tensorflow給出了定點化的Op操作,下面我將詳細介紹Tensorflow平臺的定點化流程,如圖7所示。
輸入數據為浮點數類型,第一經過QuantizeV2節點,得到量化后的數據,該節點實際輸出有三個:量化數據,最大值,最小值。即通過這三個數據即可恢復原始浮點數;第二進行量化的卷積操作,輸入為量化數據、數據的最大值最小值、量化參數、參數的最大值最小值,共6個,輸出有3個,量化卷積結果(32-bit整數)、量化結果的最大值和最小值;第三,量化結果與其范圍輸入到Requantize節點,做復量化,目的在于將32-bit整數重新量化成8-bit整數;第四,經過Dequantize節點,將8-bit整數還原成浮點數類型。實際上這種單元的輸入與輸出仍是浮點數,那么我們是否可以將網絡完全轉化為整數的運算呢?這就是tensorflow定點化的最后一步:
在對所有卷積做上述量化操作后,遍歷整個網絡,倘若存在Dequantize節點與QuantizeV2節點相鄰的情況,就刪掉這兩個相鄰節點,如圖7(b)所示。所以最終網絡完成了由浮點數到整數的轉變
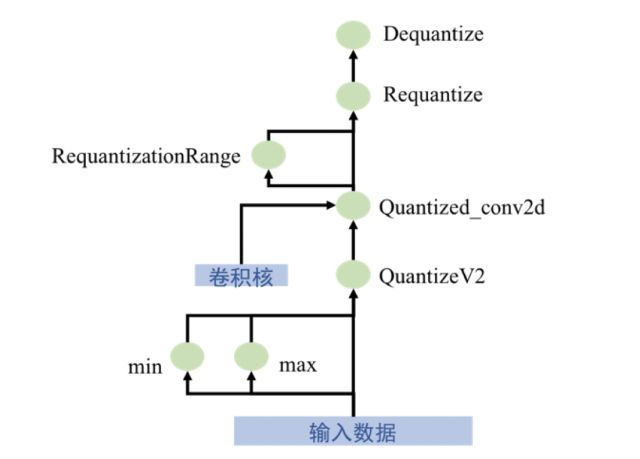
(a)運算單元

(b)去除冗余節點
圖7 tensorflow量化計算過程
注意:經過筆者的實驗,Tensorflow在移動端的Tensorflow
Lite,就是利用上述的方法,專門針對移動設別的硬件條件做了優化,定點化的模型實際有4倍的提速。但是筆者在PC端使用定點化量化模型,雖然壓縮效果不錯,但并沒有提速效果,網絡前向傳遞速度反而有下降,筆者在Tensorflow社區與github中進行了調查,也有很多研究者遇到了相同的問題,且并沒有很好的解釋,如果有讀者經過實驗驗證了定點化在PC端的可行性,或可以指出問題所在,希望可以拿出來一起交流。
模型蒸餾
前三個方法是在一個特定模型結構的基礎上,對網絡進行壓縮和加速,而模型蒸餾則“劍走偏鋒”直接設計了一個簡單結構的小網絡,那小網絡的準確率怎么和大網絡比呢?Hinton前輩提出了一個非常簡單且有效的方法——網絡蒸餾。主要思想是用預訓練好的網絡(通常結構較復雜,準確率較高),來指導小網絡的訓練,并使小網絡達到與復雜網絡相近的準確率。大網絡類比于老師,小網絡類比于學生,老師經過漫長時間的“訓練”摸索出一套適用于某個任務的方法,于是將方法提煉成“知識”傳授給學生,幫助學生更快地學會處理相似的任務。整個思想中最大的難題在于如何有效地表達“知識”,并有效地指導小網絡的訓練。其整體結構如圖8所示
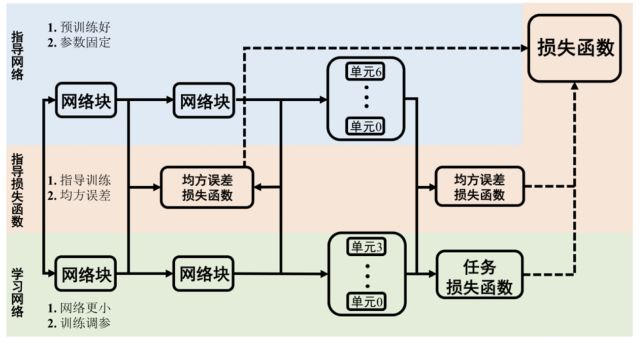
圖8 模型蒸餾結構
圖中藍色部分為教師網絡,網絡參數由預訓練好的參數初始化,并在訓練過程中固定;綠色部分為學生網絡,網絡結構相對簡單,通過訓練學習參數;紅色部分為指導損失函數,一般選取均方誤差損失函數,用于指導學生網絡學習教師網絡的輸出。原網絡由相似結構的網絡塊組成,每個網絡塊中有若干個單元,小網絡和大網絡包含相同個數的網絡塊,但每個網絡塊中的單元個數比大網絡小。整個網絡的損失函數包括原本任務的損失函數,和大網絡對小網絡的指導損失函數,其中指導損失函數為每個網絡塊輸出特征圖的均方誤差,如下式所示
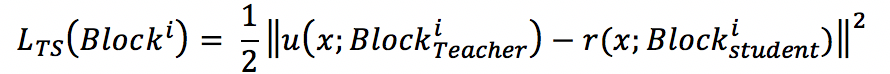
式中`L_(TS)(Block^i`)`表示第i個網絡塊位置處的指導損失函數;`u`(x`;Block^i_Teacher)`表示大網絡在第i個Block處的輸出特征圖:`r`(x`;Block_(Teacher)^i))`表示小網絡在第i個網絡塊處的輸出特征圖。整體網絡的損失函數如下式所示。

式中`L_(orig)`為直接訓練網絡的損失函數;λ為提前設定的超參數,表示大網絡對小網絡指導損失函數的重要性;N表示參與指導的網絡塊個數。
模型蒸餾的重點參數是λ,代表了指導損失函數的重要性,對不同網絡結構,不同訓練任務,需要設置不同的λ。實際上針對不同的任務和網絡,λ參數的值是不同的,但λ參數選取十分必要。
1. 當λ過小時,總損失函數與原損失函數幾乎相同,總損失函數對各參數的更新值幾乎全部取決于原任務損失函數對各參數的導數,這種訓練與非蒸餾模型的訓練相差不多,此時將存在兩種問題:
a. 當指導損失函數可以調整參數至更優解時,由于λ參數過小,參數在指導損失函數調整方向的步長過小,所以無法引導參數向更優解處調整。
a. 當原任務損失函數可以調整參數至更優解時,由于λ參數的存在,將使參數偏離更優解處調整,無法達到實際更優解。
2. 當λ過大時,總損失函數與指導損失函數幾乎相同,每次迭代的參數更新值幾乎全部取決于指導損失函數,這種訓練將完全陷入模仿訓練誤區。此時,小網絡學習重點偏向于模仿大網絡而忽略了任務本身,導致實際訓練效果下降甚至發生錯誤。
經過筆者的實驗,經驗性地發現,需要設置合適的使指導損失函數約等于且不大于任務損失函數時(每次迭代訓練中損失函數的值是動態變化的,約等于且不大于是統計意義上的),訓練得到的小網絡效果最好。如果讀者有不同的發現或理論推導,希望可以一起交流。
除λ外,筆者通過實驗也發現訓練模式對模型蒸餾的效果有很大的影響。在訓練蒸餾網絡時,兩個損失函數聯合訓練,也可能導致收斂變慢的問題。由于小模型的特征空間維度小于大模型,兩個模型參數的最優參數有一定的差異,因此若在某一次迭代訓練過程中,若兩個損失函數對參數求導得到的方向不同,則每個參數更新得到的新參數即無法向正常損失函數的極小值處更新,也無法向指導損失函數的極小值處更新;當兩個損失函數對參數求導得到的方向恰好相反時,可能導致參數的實際更新值非常小,最終在很長一段訓練中陷入該點。
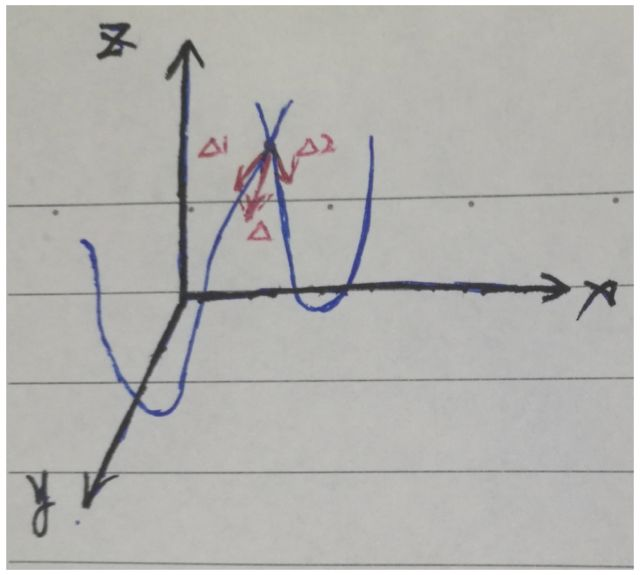
圖9 兩個損失函數的相互誤導
如圖9所示為兩個損失函數的相互誤導,假設僅有x,y兩個參數,z方向代表損失函數的值,兩個藍色線分別表示指導損失函數與任務損失函數與x,y兩個參數的關系,設某次迭代前,參數恰好到了兩條線的交點,即兩個損失函數相等(實際中很難這樣),紅色箭頭表示向量,是兩個損失函數更新的方向和大小,那么參數的實際更新大小和方向即為兩個向量的和,其方向可能并不是向參數最優解更新。當參數個數更多時,參數空間更加復雜,更容易引起訓練的錯誤。
筆者經過實驗,發現如果先單獨對指導損失函數進行訓練,然后再加入任務損失函數聯合訓練,得到的模型效果將會比直接聯合訓練得到的模型好很多。如果讀者有不同的發現或理論推導,希望可以一起交流。
其實現如今的研究工作中,對模型蒸餾沒有很成熟的理論支撐,大多研究也僅是以形而上的方式,類比Hinton提出的方法。尤其在損失函數設計和指導位置選取上,并沒有明確的說明,只是經驗性地使用均方誤差為損失函數(表達兩個特征圖或特征向量的距離),選取網絡最后一層特征向量或特定結構的輸出特征圖作為指導位置。所以模型蒸餾方法仍有很大的研究空間。
總結
本文介紹了比較常見的4種卷積神經網絡壓縮和加速方法,其中網絡裁枝與低秩估計的方法從矩陣乘法角度,著眼于減少標量乘法和加法個數來實現模型壓縮和加速的;而模型量化則是著眼于參數本身,直接減少每個參數的存儲空間,提升每次標量乘法和加法的速度,從而實現模型的壓縮和加速;模型蒸餾方法卻是從宏觀結構入手,直接構造了結構簡單,參數少的小網絡,將難點轉移成對小網絡的訓練上。
在實際應用中針對特定的網絡模型,這些方法可以互相融合,同時處理一個網絡。甚至對于一些較深層的網絡,可以在某些層使用裁枝方法,在其他層使用低秩估計方法。對卷積神經網絡模型壓縮和加速的研究才剛剛開始,還有很多值得探索的方法有待挖掘。
參考文獻
[1]He Y, Zhang X, Sun J. Channel pruning for accelerating very deep
neural networks[C]//International Conference on Computer Vision (ICCV).
2017, 2: 6.
[2]Cheng J, Wang P, Li G, et al. A Survey on Acceleration of Deep
Convolutional Neural Networks[J]. arXiv preprint arXiv:1802.00939, 2018.
[3]https://blog.csdn.net/yixianfeng41/article/details/73009210
[4]http://www.xiongfuli.com/%E6%9C%BA%E5%99%A8%E5%AD%A6%E4%B9%A0/2016-06/tensor-decomposition-tucker.html
[5] Hinton G, Vinyals O, Dean J. Distilling the knowledge in a neural network[J]. arXiv preprint arXiv:1503.02531, 2015.
[6] Romero A, Ballas N, Kahou S E, et al. Fitnets: Hints for thin deep nets[J]. arXiv preprint arXiv:1412.6550, 2014.
[7] Kim J, Park S U K, Kwak N. Paraphrasing Complex Network: Network
Compression via Factor Transfer[J]. arXiv preprint arXiv:1802.04977,
2018.
[8] Li Q, Jin S, Yan J. Mimicking Very Efficient Network for Object
Detection[C]//2017 IEEE Conference on Computer Vision and Pattern
Recognition (CVPR). IEEE, 2017: 7341-7349.
[9] Wei Y, Pan X, Qin H, et al. Quantization Mimic: Towards Very Tiny
CNN for Object Detection[J]. arXiv preprint arXiv:1805.02152, 2018.
[10] Mehta R, Ozturk C. Object detection at 200 Frames Per Second[J]. arXiv preprint arXiv:1805.06361, 2018.